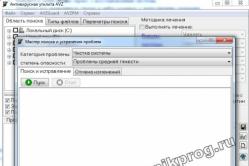
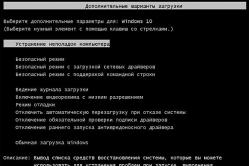
Zharoznizhuvalny for children is recognized as a pediatrician. Allegedly, there are situations of inconspicuous help in case of danger, if the child is in need of giving innocently. Todi dad take on the versatility and constipation of fever-lowering drugs. How can you give children a breast? How can you beat the temperature of older children? What are the best ones?
Ti is not a slave!
Zakritiy polish course for children of elite: "Spravzhnє oblastuvannya svitu".
http://noslave.org
Material z Wikipedia
The Laplace operator is equivalent to the last taken of the gradients and divergences: texvc NO knowledge; Math / README - fine tuning.): \ Delta = \ operatorname (div) \, \ operatorname (grad) In such a rank, the value of the Laplace operator at the point can be considered as the density of the dzherel (sinks) of the potential vector field It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ \ Operatorname (grad) F at ts_y points. In Cartesian coordinate systems, the Laplace operator is often referred to as It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Div. math / README - completion of the adjustment.): \ Delta = \ nabla \ cdot \ nabla = \ nabla ^ 2, tobto yak scalar create operator nabla on yourself. The Laplace operator is symmetric.
Less than the value of the Laplace operator
Operator Laplace є the natural health care functions of the decile of the winter and the other of the same fun. Just as function It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F (x) maє at the outskirts of the point It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ X_0 I will go to my friend without interruption It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F "" (x) those like the price tag of Taylor's formula
texvc NO knowledge; Math / README - completion of the adjustment.): \ F (x_0 + r) = f (x_0) + rf "(x_0) + \ frac (r ^ 2) (2) f" "(x_0) + o (r ^ 2), at It’s hard to rozibrati viraz (vikonuvaniy file texvc
,
It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - completion of the adjustment.): \ F (x_0-r) = f (x_0) -rf "(x_0) + \ frac (r ^ 2) (2) f" "(x_0) + o (r ^ 2), at It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - add-on from the set.): R \ to 0,
friend is abducted є meza
It’s hard to rozibrati viraz (vikonuvaniy filetexvc NO knowledge; Math / README - completion of the adjustment.): \ F "" (x_0) = \ lim \ limits_ (r \ to 0) \ frac (2) (r ^ 2) \ left \ (\ frac (f (x_0) + r) + f (x_0-r)) (2) -f (x_0) \ right \).
Yaksho, go to the function It’s hard to rozibrati viraz (vikonuvaniy file texvc from It’s hard to rozibrati viraz (vikonuvaniy file texvc wintry, screw it this way, tobto for a given point It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - completion of the adjustment.): M_0 (x_1 ^ 0, x_2 ^ 0, ..., x_k ^ 0) look at It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ K-mirnu kulova near It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little bit about the adjustment.): \ Q_r radius It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little bit about the adjustment.): \ Rі difference between arithmetic mean
texvc NO knowledge; Math / README - finishes adjusting.): \ Frac (1) (\ sigma (S_r)) \ int \ limits_ (S_r) Fd \ sigma
functions It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F on the cordon It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little bit about the adjustment.): \ S_r such outskirts with a cordon area It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ \ Sigma (S_r) that value It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little bit about the adjustment.): \ F (M_0) near the center of the center It’s hard to rozibrati viraz (vikonuvaniy file texvc , then if there is no interruption to other private old functions It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F on the outskirts of the point It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little bit about the adjustment.): \ M_0 meaning laplasian It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - add-on from the set.): \ \ Delta F u tsіy totsі є boundary
texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta F (M_0) = \ lim \ limits_ (r \ to 0) \ frac (2k) (r ^ 2) \ left \ (\ frac (1) (\ sigma ( S_r)) \ int \ limits_ (S_r) F (M) d \ sigma -F (M_0) \ right \).
One hour in advance for the operator Laplace function It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F, scho can without interruption of other origins, the following formula is valid
texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta F (M_0) = \ lim \ limits_ (r \ to 0) \ frac (2 (k + 2)) (r ^ 2) \ left \ (\ frac (1 ) (\ omega (Q_r)) \ int \ limits_ (Q_r) F (M) d \ omega -F (M_0) \ right \), de It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little more on the adjustment.): \ Omega (Q_r)- obsyag of the outskirts It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - add-on from setup.): \ Q_r.
The tsia formula bends without the middle link of the Laplace function with the common middle on the outskirts of the central point.
The proof of the number of formulas can be found, for example, at.
Infectious depressions, in all cases, if the stench smells, it can be assigned to the operator Laplace function It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little more on the adjustment.): \ F. Also, the value of overriding the extraordinary value of the Laplace, as well as the transfer of other obsolete functions, to be looked at, and to be taken into account for the important values in case of the uninterrupted nature of the older ones.
Vislovyuvannya for the Laplace operator in different curved coordinate systems
At fairly orthogonal curved coordinates at trivial space It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Div. math / README - completion of the adjustment.): q_1, \ q_2, \ q_3
:
texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta f (q_1, \ q_2, \ q_3) = \ operatorname (div) \, \ operatorname (grad) \, f (q_1, \ q_2, \ q_3) =
It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - fine tuning.): = \ Frac (1) (H_1H_2H_3) \ left [\ frac (\ partial) (\ partial q_1) \ left (\ frac (H_2H_3) (H_1) \ frac (\) partial f) (\ partial q_1) \ right) + \ frac (\ partial) (\ partial q_2) \ left (\ frac (H_1H_3) (H_2) \ frac (\ partial f) (\ partial q_2) \ right) + \ frac (\ partial) (\ partial q_3) \ left (\ frac (H_1H_2) (H_3) \ frac (\ partial f) (\ partial q_3) \ right) \ right], de It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): H_i \- Coefficacy Lame. Cylindrical coordinates
Cylindrical coordinates have a straight posture It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - add-on from the set.): \ R = 0
:
texvc NO knowledge; Math / README - fine tuning.): \ Delta f = (1 \ over r) (\ partial \ over \ partial r) \ left (r (\ partial f \ over \ partial r) \ right) + (\ partial ^ 2f \ over \ partial z ^ 2) + (1 \ over r ^ 2) (\ partial ^ 2 f \ over \ partial \ varphi ^ 2)
Spherical coordinates
In spherical coordinates, the pose is cob-sided (in the trivial space):
It’s hard to rozibrati viraz (vikonuvaniy filetexvc NO knowledge; Math / README - fine tuning.): \ Delta f = (1 \ over r ^ 2) (\ partial \ over \ partial r) \ left (r ^ 2 (\ partial f \ over \ partial r) \ right) + (1 \ over r ^ 2 \ sin \ theta) (\ partial \ over \ partial \ theta) \ left (\ sin \ theta (\ partial f \ over \ partial \ theta) \ right) + (1 \ over r ^ 2 \ sin ^ 2 \ theta) (\ partial ^ 2 f \ over \ partial \ varphi ^ 2)
It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta f = (1 \ over r) (\ partial ^ 2 \ over \ partial r ^ 2) \ left (rf \ right) + (1 \ over r ^ 2 \ sin \ theta) (\ partial \ over \ partial \ theta) \ left (\ sin \ theta (\ partial f \ over \ partial \ theta) \ right) + (1 \ over r ^ 2 \ sin ^ 2 \ theta) ( \ partial ^ 2 f \ over \ partial \ varphi ^ 2).
At the same time It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ F = f (r) v n-worldly space:
texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta f = (d ^ 2 f \ over dr ^ 2) + (n-1 \ over r) (df \ over dr).
Parabolic coordinates
In parabolic coordinates (in trivial space), the pose is cob-like:
It’s hard to rozibrati viraz (vikonuvaniy filetexvc NO knowledge; Math / README - completion of the adjustment.): \ Delta f = \ frac (1) (\ sigma ^ (2) + \ tau ^ (2)) \ left [\ frac (1) (\ sigma) \ frac (\ partial) (\ partial \ sigma) \ left (\ sigma \ frac (\ partial f) (\ partial \ sigma) \ right) + \ frac (1) (\ tau) \ frac (\ partial) (\ partial \ tau ) \ left (\ tau \ frac (\ partial f) (\ partial \ tau) \ right) \ right] + \ frac (1) (\ sigma ^ 2 \ tau ^ 2) \ frac (\ partial ^ 2 f) (\ partial \ varphi ^ 2)
Cylindrical parabolic coordinates
At the coordinates of the parabolic cylinder, the pose is cob to the side:
It’s hard to rozibrati viraz (vikonuvaniy filetexvc NO knowledge; Math / README - completion of the adjustment.): \ Delta F (u, v, z) = \ frac (1) (c ^ 2 (u ^ 2 + v ^ 2)) \ left [\ frac (\ partial ^ 2 F) (\ partial u ^ 2) + \ frac (\ partial ^ 2 F) (\ partial v ^ 2) \ right] + \ frac (\ partial ^ 2 F) (\ partial z ^ 2).
Zagalny crooked coordinates and Riemannian space
Drive on a smooth business relationship It’s hard to rozibrati viraz (vikonuvaniy file texvc the local coordinate system is given It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): G_ (ij)- rimaniv metric tensor on It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): X, tobto ma viglyad metric
texvc NO knowledge; math / README - completion of the adjustment.): ds ^ 2 = \ sum ^ n_ (i, j = 1) g_ (ij) dx ^ idx ^ j
.
Significantly through It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): G ^ (ij) matrix elements It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): (G_ (ij)) ^ (- 1)і
texvc NO knowledge; math / README - completing the adjustment.): g = \ operatorname (det) g_ (ij) = (\ operatorname (det) g ^ (ij)) ^ (- 1)
.
Vector field divergence It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a little more on the adjustment.): F given by coordinates It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - completion of the adjustment.): F ^ i(I represents the first-order differential operator It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - completion of the adjustment.): \ Sum_i F ^ i \ frac (\ partial) (\ partial x ^ i)) on rіznomanіttі X reckon with the formula
texvc NO knowledge; Math / README - completion of the adjustment.): \ Operatorname (div) F = \ frac (1) (\ sqrt (g)) \ sum ^ n_ (i = 1) \ frac (\ partial) (\ partial x ^ i ) (\ sqrt (g) F ^ i)
,
and the components of the gradation of the function f- for the formula
It’s hard to rozibrati viraz (vikonuvaniy filetexvc NO knowledge; Div. math / README - completion of the adjustment.): (\ nabla f) ^ j = \ sum ^ n_ (i = 1) g ^ (ij) \ frac (\ partial f) (\ partial x ^ i).
Operator Laplace - Beltramі on It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): X
:
texvc NO knowledge; Math / README - completion of the adjustment.): \ Delta f = \ operatorname (div) (\ nabla f) = \ frac (1) (\ sqrt (g)) \ sum ^ n_ (i = 1) \ frac (\ partial) (\ partial x ^ i) \ Big (\ sqrt (g) \ sum ^ n_ (k = 1) g ^ (ik) \ frac (\ partial f) (\ partial x ^ k) \ Big).
Value It’s hard to rozibrati viraz (vikonuvaniy file texvc NO knowledge; Math / README - a clue about the adjustment.): \ Delta fє a scalar, so that you don’t change the hour of changing the coordinates.
Gagging
With the help of the given operator, manually write down Laplace's, Poisson's and hvilyove's rivnyannya. The physical operator Laplace is stagnant in the electrostatic and electrodynamics, the quantum mechanics, in the modern physics of the suction mediums, as well as in the case of the implantation of membranes, the floats and the surface of the diaphragms. , at the bezperervnuyu border, to the wicked men of Laplace and Poisson, who do they go to the house.
Options and hospitality
- The D'Alembert operator is a reference to the Laplace operator for hyperbolic people. I will turn on my friend for an hour.
- The vector Laplace operator is the reference of the Laplace operator to the type of vector argument.
Div. also
Write a guide about the article "Laplace Operator"
Literature
Posilannya
| |||||||||||||||||||
The Laplace operator is a differential operator, which is a line space smooth functions and denoted by a symbol. Functions F win set at the same function
The Laplace operator is equivalent to the last one taken from the city and divergence operations.
Gradient is a vector that shows directly the growth of a certain value, meaning that it changes from one point to the point (scalar field). For example, if you take the surface of the Earth over the ditch of the sea, then the gradation at the skin points of the surface will show "straight to the best of the world." Size (modulus) of the gradation vector for road traffic growth. For a trivial space, a vector function with components is called a gradient, deyaka is a scalar function of coordinates x, y, z.
If - the function of n changes, then the n-world vector is called a gradient.

Components that can be delivered privately for all arguments. Gradient means grad, or from the visibility of the operator nabla,
The value of the gradinta vipliv, scho:
The sense of the gradation of a scalar function f is that a scalar TV with an indefinitely small vector of displacement gives an additional differential of the function of a variable coordinate change in the open space f, for some reason zagalny encampment wona f golovna) part of the change f at the substitution. Vikoristovuchi one of the same letter for the designated function of the vector and the secondary function of the coordinates, you can write:
Worth respect here, well, that the formula for the general differential does not lie in the form of coordinates xi, because of the nature of the parameters in x in zagal, then the differentiation of the differential is invariant, so that it is a scalar, if there are any changes in the vectors, but rank, to appear as a step vector, to be a vector, represented in a dual basis, which only and can give a scalar for a simple summation of the creation in the coordinates of an invariable (contravariant), so that a vector, we write down in an invariant basis.
In such a rank, viraz (apparently - for rather curved coordinates) can be completely correct and invariably written as:
Or I omit the sumi sign after Einstein's rule,
Divergence is a differential operator, which imaging a vector field on a scalar (so that the differentiation operation, as a result of the stagnation of a scalar field to the vector field), which is the beginning (for a skin point), more precisely - there are no more incoming and outgoing flows).
If the flow can be attributed with an algebraic sign, then there is no need to change the incoming and outgoing flows okremo, everything will be automatically secured when the sign is raised. This can be given a shorter value for the divergence:
divergence - a differential operator on a vector field, which characterizes the potential of this field through the surface of the small outskirts of the skin internal point of the area of the field.
The divergence operator, stuck to field F, means yak abo
The meaning of the divergence of the viglyad is as follows:
de ФF - the flow of a vector field F through a spherical surface with an area S, but it will be surrounded by a strip V. It is also more zagalny, that is, it is important if the shape of an area with a surface S and a general V is allowed to be good. Alone, I move around the middle spheres with a radius, which is less than zero. The value, on the view from the pointed below, is not tied to the singular coordinates, for example, Cartesian ones, which can represent the additional animation in singing vipads. (For example, if you vibrate around a cube shape or a parallelepiped, it is easy to use formulas for Cartesian coordinates, pointing in the offensive paragraph).
by such a rank, the meaning of the Laplace operator at the point can be the same as the density of the dzherel (sinks) of the potential vector field gradF at the point. In Cartesian coordinate systems, the Laplace operator is often referred to as in the view of the scalar operator nabla on itself.
Laplace operator
The Laplace operator starts with a viraz
and in the Cartesian coordinate system is described by the formula

We know the viraz for the Laplace operator in curved orthogonal coordinate systems. For a complete recordable gradation and divergence in curved coordinate systems

Providing the time to the Laplace operator,
Application 1. Know the viraz of the Laplace operator in a cylindrical coordinate system.
Respect 1. The Laplace operator in the polar coordinate system is defined by the formula
Application 2. Know the viraz for the Laplace operator for coordinate systems.
Decision. The value of the performance in the Lame is given,
Rivnyannya Laplace
Rivnyannyam Laplace is called rivnyannya mind.
The price of the food is called the food type. It is often found at the staff, tied because of the potential of the new stationary fields. Zokrema, zavdannya viznachennya temperature field, electrical potential, spring forces and deformations are tied to the definitions of Laplace's rivnyannya. Significantly, in mathematical physics, there is also a comparison of the hyperbolic and parabolic type.
isnu bagato different methods the development of the food type. Among them, you can see the method of subtle changes, the method of function of the dzherel, the theory of potential, the method of analitical functions and the rich. A few of the simplest workshops, which are knitted from special methods, are easy to understand.
Cylindrical symmetry. We know the solution of Laplace's function, which is a cylindrical symmetry, tobto. do not lie in the polar kut and wandering z. At the same time, Laplace's name is written in a cylindrical coordinate system, maє viglyad

Private used here are replaced by new ones. Ryvnyannya viplya
de - dovіlnі postіynі, as can be known from the border minds.
Spherical symmetry. We know the solution of Laplace's function, which is spherical symmetry, tobto. do not lie down from the huts. In general, the name of Laplace, written in spherical coordinate systems, maє viglyad

It doesn’t matter to know
Poisson adjustment can be seen on specific stocks.
Application 1. To know the decision of Poisson's line in the middle of the cola radius, where
Decision. Shukan's function is a large cylindrical symmetry, which can be written down to Poisson's equation in a cylindrical coordinate system at a viglyad

Virishimo tse rivnyannya
gradient curved lamina differential
Permanently that is known from the borderline and between the functions. Vrahoyuchi, scho otrimaєmo. Wash otrimaєmo
Otzhe, maєmo residual view
laplasian, is a differential operator, which is started by the formula
(here - coordinates in), as well as deyakі yogo zagalnennya. L. o. (1) є simplest eliptic. differential operator of the 2nd order. L. o. the role of mathematics is important. analysis, math. physics and geometry (div., for example, Laplace Rivnyannya, Laplace - Beltram Rivnyannya, Harmony function, Harmony form).
Nekhai Pomsta n-world rimanovy space with metric
nehai - matrix, ringing up to matrix ![]() Todi L. o. (abo the Laplace - Beltram operator) of the Riemannian metric (2)
Todi L. o. (abo the Laplace - Beltram operator) of the Riemannian metric (2)
de ![]() - local coordinates on M. Operator (1) bears the sign of L. o. standard Euclidean metric
- local coordinates on M. Operator (1) bears the sign of L. o. standard Euclidean metric
Usage of operator (3) є L. o. on differential forms. Itself in the vastness of all known differential forms on the ML. O. ma viglyad
de d - operator of the most recent form differentiation, d * - formally, a statement to the operator, which is to start for an additional offensive creature on smooth financial forms:
de * is the Hodge operator, generated by the metric (2) and the transferє of the p-form ( etc) -form. In formulas (5), the form a and b are used for action; on complex forms, it is necessary to use a scalar extension (5). The sounding of the operator (4) on the O-shape (that is, a function) is given by formula (3). On p-forms with a sufficient whole L. o. local coordinates write yak

Here - covariant
Curvature tensor - Річчі tensor. Nekhay given a decent eliptic. complex
de E p - design for complex development on business development M, G (E p) -
the vastness of smooth transitions in the skin E p the ermit metric, as well as adding an element of sufficient rank to the M, it is possible to have a scalar-ermitic tvir in the vastness of smooth financial breaks in development Єp. Todi is assigned by the operator d *, formally linked with operators d. Formula (3) will be followed by L. o. on the skin space Г ( E p).
If the complex (6) takes the de Rham complex, then with the natural vibration of the metric in the p-forms and the element of the obsyag, generated by the metric (2), take the L. o. de Rama's complex of descriptions of L. o. on forms.
On the complex development of the complex de Rama є eliptic. complexes

de - space of smooth forms like ( p, q). on M. Introduce the ermitic structure in a dotted shape on M, you can stay L. about. (4) the complex de Rama and L. o. complex (7), (8):

Kozhen z cich operators to translate the space Yaksho M - Kehler's
An important fact is that the role of L. o. eliptic. complex, є Morthogonal distribution:
At the ts'omu raskladі de - L. o. complex (6), so there is a space of "harmonious" E p(in the case of the de Rama complex - the space of the more harmonious forms of the step p). Direct sum of the first two completions near the right part of the formula (9) ![]() but the straight sum is two remaining dodanks to get out of
but the straight sum is two remaining dodanks to get out of ![]() Zokrem, spreading (9) gives an isomorphism to the space of the cohomology complex (6) at the member and to the space of harmonies. perereziv
Zokrem, spreading (9) gives an isomorphism to the space of the cohomology complex (6) at the member and to the space of harmonies. perereziv
Lit.: Ram J. de, Differentsiyovany riznomanittya, prov. s French., M., 1956; Zhen Shen-Shen, Complex development, prov. from English, M., 1961; Wells R., Differential calculation on complex business transactions, prov. s English, M., 1976. M. A. Shubin.
- - the integral to the point of permanent mass m in the field of the Newton - Coulomb potential L = - the moment to the pulse is the initial area of the orbit, and at the same time with the integral of energy - the configuration.
Mathematical encyclopedia
- - 1) Integral view of the integral Laplace of the transformation of the function f. Bulo is seen by P. Laplace at the book. 18-hour 19 Art.
Mathematical encyclopedia
- - asymptotic estimates - the method of calculating the asymptotics for l & gt ...
Mathematical encyclopedia
- - the consistency of the congruence in the trivial projective space, in the two skin congruences made similar to the two families of lines obtained by the same surface ...
Mathematical encyclopedia
- - Laplace's transformation, - in a wide sense - Laplace's integral kind of deintegrating is carried out behind a certain contour L in the area of a complex change z, so that the function f ...
Mathematical encyclopedia
- - installed by P. Laplace accumulation of capillary vise Pq from time to time. the curvature of the surface is broken between the phases and the surface tension q: Pq = eq.
- - Linear differential. operator, which f-tsії f put in the version of the f-tsіy Estrіchaєtsya in pl. zavdannya mat. physics. Ur-nya delta f = 0 stars. Laplace Rivnyannyam ...
Natural science. Encyclopedic vocabulary
- - One z main. the laws of capillary manifestations Sgidno z L. z., the growth of p0 hydrostatic ...
- - Line differential ...
Great encyclopedic polytechnic vocabulary
- - Primorsk region, Pivdenno-Ussuriy region, on the Uzbek coast of Pivn.-Sea of Japan, between misami Avsenka and Durinina, on the edge of Shkhadgou bay ...
Encyclopedic Dictionary of Brockhaus and Evfron
- - geodesic azimuth A directly to the point, which is to be spared, rejecting the astronomical azimuth α, correcting from the urahuvannya in flux to the point of caution ...
- - the cosmogonic hypothesis about the establishment of the Sonya system - the Sontsya, the planets and their companions from the gas nebula, how to wrap around and shrink, was captured by P. Laplace in 1796 in the popular book "Viklad ...
Velyka Radianska Encyclopedia
- - the accumulation of the differential of the hydrostatic vice Δp on the surface of the break of two phases from the interphase surface tension σ and the average curvature of the surface ε at the point where it can be seen: Δр = р1-р2 = εσ, de p1 -...
Velyka Radianska Encyclopedia
- - Laplace, delta-operator, Δ-operator, linear differential Operator, which is a function φ from n changes x1, x2 ,.
Velyka Radianska Encyclopedia
- - installed by P. Laplace fallowness ????? - A capillary vise? from the middle curvature E of the surface to the phase separation, how to intercut, and to the surface tension?
- - Laplace operator - line differential operator, what function? to put in a kind of function Рівняння ??? 0 to be called Laplace рівняння ...
Great encyclopedic vocabulary
"LAPLASA OPERATOR" by books
Laplace display
3 Laplace books the authorSPADCHINA LAPLASU
3 Laplace books the author Vorontsov-Velyaminov Boris MikolayovichZukor Laplace
3 books History of old and recent the author Arnold Volodymyr IhorovichTsukor Laplace's History of F. Arago: in his youth, having drunk at full time, at the time of vicuples (like an Englishman in Egypt?), Turning, becoming the most active student, praising with Ampere and in optics. Yogo was hung up to the Academy of Sciences. The candidate (dosi) can see all the voices that
Laplace's principle
3 Yak books are far from tomorrow the author Moiseev Mikita MikolajovichLaplace Principle I do not want to become a virtual one, but I do not re-create an atheist. I greeted me, if I were categorically firm in the spheres, I would lie on the border of the mind and my emotions are inconsistent. Everything is unproven. Zhodna logic is not suitable for a virgin food.
Demon Laplace
More, less you know. An unprecedented glance at the light of finance author Mobussin MichaelDemon Laplace 200 years ago in science panuvav determinism. They looked at Newton’s insights and looked at everything like that of the year’s mechanism. The French mathematician P'єr Simon Laplace has kindly grasped the essence of determinism in his famous work "Dosvid of Philosophy
43. Demon, Laplace
3 books Philosopher on the edge of Vsesvita. NF-Philosophy, Abo Hollywood Idea for Help: Philosophical Problems in Science Fiction Films by Rowlands Mark43. Demon, Laplace Hypothetical hopefulness, which is able to know about the state of All-Sight and is built on the basis of the exact transmission of the mighty serpent. Guess hocha b prol iz " Especially thoughts": Yakby stench could not only bachiti maybutni
Laplace azimuth
VіkіpedіyaLaplace hypothesis
3 books by Velyka Radianska Encyclopedia (LA) of the author BSE author Mayers ScottRule 52: If you wrote the operator new with the modifications, write and the general operator delete Operators new and delete are not often used with modifications in C ++, because, as you don’t know, there is nothing terrible. Guess (rules 16 and 17), if you write like this
1. Operator Select - the basic operator of mov and structured feeds
Bazi Danikh's books: lecture notes the author Author nevidomy1. Operator Select - the basic operator of movable structured feeds. The central point of moving structured feeds is SQL, the Select operator is borrowed, with the help of which it is possible to implement the required operation per hour of robots with databases - queries. Operator Select
15.8.2. Operator new () and operator delete ()
3 C ++ books for pochatkivtsiv author Lieppman Stanley15.8.2. Operator rewinding new () and operator delete () The member operator new () can be rewangled for another reason, but all the naked may change lists of parameters. The first parameter is due to the mother type size_t: class Screen (public: void * operator new (size_t); void * operator new (size_t, Screen *); // ...); Інші parameters
We looked at three basic operations of vector analysis: calculating gradtx for a scalar field a ma rot for a vector field a = a (x, y, z). Tsi operations can be recorded in big simple viglyadі for the additional symbolic operator V ("nabla"): Operator V (Hamilton operator) is both differential and vectorial power. Formally, multiplying, for example, multiplying ^ on the function і (x, y), we will make a private differentiation: Within the framework of vector algebra, formal operations on the operator V are carried out in the same way as a vector. Victorist formalism, the following basic formulas are recognized: 1. As a scalar function, to differentiate, then according to the rule of multiplying a vector by a scalar, P, Q, R - differentiation of an operator Laplace Understand about curved coordinates Spherical coordinates 3. Computable vector tvir post-term functionsі = negligible and for a post-vector vector we will assume three separate powers for a scalar and vector creatures. We got used to it, but the operator is V for all values, written yo. In tsomu sense, for example, it is a scalar differential operator. Zastosovuchi operator V to create any values, need mother on respect a rule of thumb Differentiation to the Creator. Supplement 1. Bring, for formula (2) with respect to 1, we can deny whether it means that the fact that "obl" is not just a value that can be included in the foldable formula, the value is meant by the index z ("const" )), but the residual result will go down. Application 2. Do u (xty, z) is a scalar function that differentiates, and (x, y, z) is a vector function that differentiates. To bring the 4 Rewrite the left part (8) in the symbolic viglyad Z look at the differential character of the operator V is recognizable. Since її is a permanent scalar, then you can blame the scalar for the sign of the scalar, so a (the index e was dropped on the last few lines). In viraz (V, ic), the operator V is only for a scalar function, and for the result we can accept the value of 2. Victor's formalism of action with the operator V as with a vector, memory is required, but V is not an exceptional vector - it is not important , nі straight, even. for example, vector)